Robert A. Calder, MD, MS; Katherine Gavinski, MD, MPH, MSEd; Jayshil J. Patel, MD
WMJ. 2024;123(5)407-411.
Epidemiology is the study of how disease is distributed, transmitted, and develops in populations. Screening and diagnostic tests help us differentiate between the people who have the disease and people who do not, but diagnostic tests may suffer from problems with validity and reliability. For example, it may be tempting to think that a positive diagnostic test means that the patient has the disease in question, but without incorporating clinical context or test characteristics, we may make an erroneous conclusion. Understanding context, such as pretest probability, and the validity and reliability of diagnostic tests are critical for clinical practice. In this column, we apply Bayes’ rule using a story-like format. We describe operating characteristics of diagnostic tests, discuss diagnostic test sequencing, and depict the receiver operating characteristic curve. Finally, we apply likelihood ratios and describe how these ratios can enrich illness scripts.
BAYES’ RULE AND APPLICATION IN A STORY-LIKE FORMAT
English clergyman Thomas Bayes derived his “rule” in the late 18th century.1 Assuming that the prevalence of disease and efficiency of the test in those with and without disease are known, Bayes’ rule allows us to predict the probability of disease by knowing only the test results. Here’s how Bayes’ rule works (Figure 1): imagine a population who are either “diseased” or “nondiseased.” Those with the disease have either a positive or a negative test for the disease, and those without disease also have a positive or negative test. Bayes’ rule informs us that the probability of disease is simply the ratio of those with the disease who have a positive test (“true positive” or TP) divided by everyone with a positive test (those who have a positive test with the disease [TP] plus those who have a positive test without the disease [“false positive” or FP]).
Over 20 years ago, Gerd Gigerenzer presented physicians with a diagnostic riddle.2 Suppose a woman has a positive mammogram. What is the probability that she has breast cancer? In this case, we assume that mammography is 90% sensitive for detecting breast cancer, the prevalence of breast cancer in the woman is 0.8%, and there is a 7% false positive percentage for mammography (93% specificity). The most common answer physicians provided was 90%.
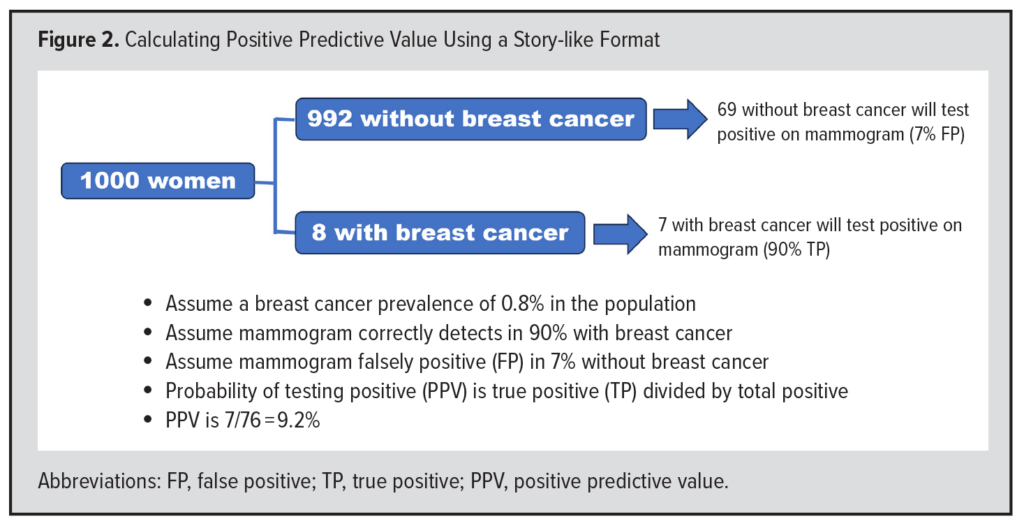Gigerenzer addressed these problems by popularizing a “story-like format” for Bayes’ rule (Figure 2). He proposed that we begin by thinking of a population of 1000 women. If the prevalence of breast cancer in this group is 0.8%, then 8 will have breast cancer and 992 will not. Of the 8 with breast cancer, approximately 7 will have a positive mammogram, since mammography is positive in 90% of patients with breast cancer (8 x 0.90 = 7.2 or approximately 7). Of the 992 without breast cancer, approximately 69 will have a positive mammogram, since 7% have a FP test (992 x 0.07 = 69.4 or approximately 69). Of the 76 total positive tests (7 + 69), 7 are TPs. The probability of having breast cancer if the test is positive, which is the positive predictive value (PPV), is the ratio of TP (7) to total positives (76), or 7/76 (9.2%). The application of Bayes’ rule using a story-like format may turn what seems like a complicated mathematical calculation into a sensical solution. Nevertheless, it is important to understand the prevalence of disease and the operating characteristics of diagnostic tests that underly the use of both Bayes’ rule and Gigerenzer’s story-like format.
THE RELATIONSHIP BETWEEN PREVALENCE AND POSITIVE PREDICTIVE VALUE
How does the prevalence of disease affect the positive predictive value of a test? Suppose that a woman who detects a breast lump on self-exam has a 20% risk of breast cancer. What is the probability she has breast cancer if she has a positive mammogram? The answer is far higher than 9%. Using the story-like format, imagine a population of 1000 women. If the prevalence of breast cancer in the population is 20%, 200 of these women will have breast cancer and 800 will not have breast cancer. Of the 200 women with breast cancer, 180 would have a positive mammogram if the sensitivity of mammogram for breast cancer is 90% (200 x 0.90 = 180). Of the 800 without breast cancer, and assuming the FP rate is 7% (if specificity of mammogram is 93%), then 56 (800 x 0.07 = 56) would have a FP test. The total number of positive tests is 236 (180 TP + 56 FP), which equates to a PPV of 76.3% (180/236). When the prevalence of disease increases from 0.8% to 20%, the PPV increases from 9% to 76% (we assumed the mammogram test had the same operating characteristics: sensitivity of 90% and FP percentage of 7%). This is a striking difference. It is the difference between using a test for “screening” purposes and “diagnostic” purposes. Screening for disease involves testing individuals in a population with a very low prevalence of disease. Diagnosis typically involves testing individuals in a population with a much higher prevalence of disease. As a result, the probability that a positive test truly represents disease is much greater when there is a higher prevalence of disease.
OPERATING CHARACTERISTICS OF DIAGNOSTIC TESTS
In an ideal world, individuals with disease would have a positive test and those without disease would have a negative test. Of course, such a world does not exist and, therefore, it is imperative to understand the operating characteristics of diagnostic tests.
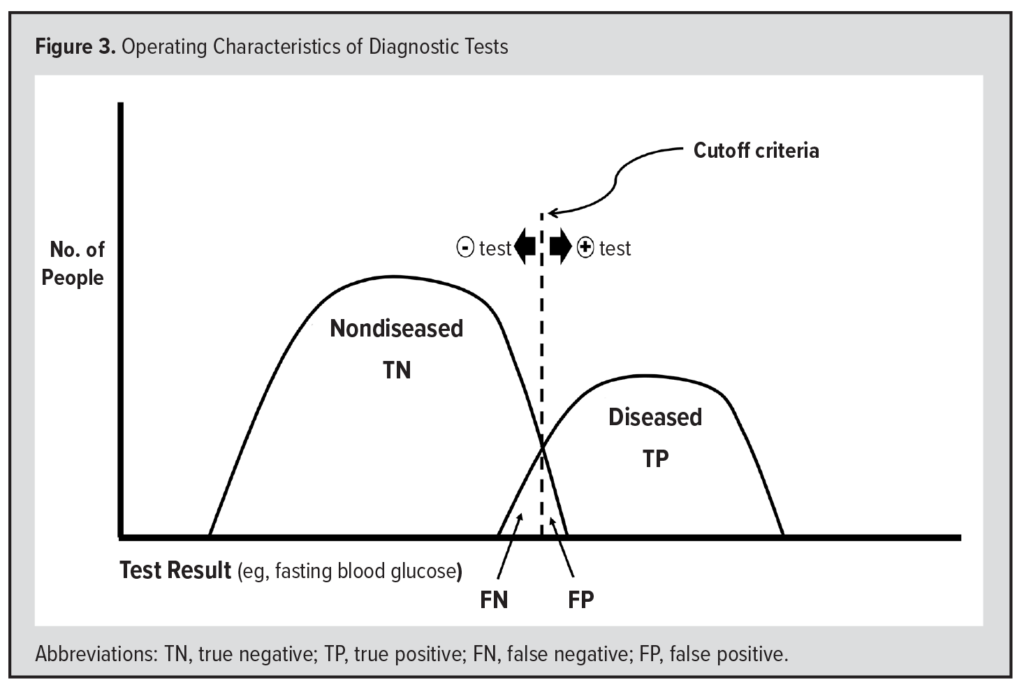Suppose we use the level of fasting blood glucose (FBG) to diagnose diabetes (Figure 3). To do this, we must define some “cutoff” level, above which the test is “positive” for diabetes. Currently, the cutoff level is 126 mg/dL. Individuals who have an FBG of 126 or greater have a positive test for diabetes. Most individuals with an FBG of ≥126 have diabetes and are considered TPs. The clinical signs of diabetes include polyuria (excessive urination), polydipsia (excessive thirst), and polyphagia (excessive appetite), and some individuals with an FBG of ≥126 mg/dL do not meet the clinical definition of diabetes, and their test results are considered FP.
Most individuals without diabetes have a negative test. Specifically, they have an FBG of 125 mg/dL or less, considered a “true negative” (TN) test result. Furthermore, these individuals do not have the clinical signs of diabetes (described above). However, some individuals with an FBG ≤125 mg/dL may meet the clinical definition of diabetes, and the result of their test is considered a “false negative” (FN). Thus, the diseased population consists of both TPs and FNs, whereas the nondiseased population consists of both the TNs and FPs.
The “sensitivity” of a test is the proportion of diseased who have a positive test. This is the proportion of the diseased to the right of the cutoff criteria in Figure 3 and is calculated as TP/(TP + FN). The “specificity” of a test is the proportion of nondiseased who have a negative test. This is the proportion of the nondiseased to the left of the cutoff criteria in Figure 3 and is calculated as TN/(TN + FP). One minus the specificity (1-specificity) of a test is the probability of having a positive test even though you truly do not have the disease (the FP) and is the proportion of the nondiseased to the right of the cutoff criteria in Figure 3.
It is worth emphasizing that the number of positive tests in a population is critically dependent on the prevalence of the disease in the population (reflected by the size of the “diseased” population in Figure 3). A higher prevalence of disease will yield more positive tests than a lower prevalence of disease, which will yield fewer positive tests. Therefore, the prevalence of disease is an extremely important factor when deciding whether a positive test represents the true presence of disease.
How could the FBG test be more sensitive (or identify more individuals with diabetes)? We would have to move the cutoff criteria lower, for example, to 100 mg/dL. The new cutoff value would ensure nearly everyone with diabetes has a positive test. However, many more people without diabetes also would have a positive test, reducing the specificity of the new cutoff value. Recall that specificity is the proportion of the nondiseased who have a negative test. If the cutoff were lower, more individuals without diabetes would have a (false) positive test. Thus, there is a tradeoff between sensitivity and specificity. Lowering diagnostic cutoff criteria would reduce specificity. Raising the cutoff criteria would reduce sensitivity (and would miss diabetes in those with the disease).
DIAGNOSTIC TEST SEQUENCING AND “RULING OUT” DISEASE
A sensitive test will be performed to “rule out” disease if the test is negative, meaning there are very few false negatives. For example, if a child has a sore throat, a rapid Streptococcal test, which has approximately 90% sensitivity for Streptococcus pyogenes,3 would likely “rule out” the probability of strep throat without the need to do a follow-up throat culture.
What happens when a highly sensitive test is positive? In these scenarios, diagnostic tests frequently are done in succession. Recall a highly sensitive test does not necessarily indicate the individual has the disease. Therefore, the positive screening test is confirmed with a more specific diagnostic test. For example, nascent testing for HIV included a rapid and highly sensitive test. If positive, it did not confirm that the individual had HIV. Instead, the positive test was followed by a much more specific test, which was more difficult to perform. To appreciate why this sequence is necessary, imagine a highly sensitive test whereby almost everyone with the disease in question tests positive. If the test is negative, then it effectively rules out the disease in question since everyone with the disease should test positive. However, having a positive test does not indicate the individual has the disease in question, and a positive test would need to be followed up with a highly specific test, which is usually negative in those without the disease.
RECEIVER OPERATING CHARACTERISTIC CURVES
The receiver operating characteristics (ROC) curves were first used during World War II to quantify predictions of radar operators differentiating enemy from allied aircraft.4 In medicine today, ROC curves quantify the extent to which a test discriminates between the diseased and the nondiseased. The ROC curve is a graph of the probability of TP to the probability of FP for various cutoff criteria of a test. For a given cutoff criteria, a certain percentage of the diseased will have a positive test (TP) and – unless the cutoff criteria are extremely high – a certain percentage of the nondiseased will also have a positive test (FP). As the cutoff criteria change, the percentage of TP and FP will change. When the cutoff criteria are extremely high, only a small percentage of the diseased will be identified with a positive test. As the cutoff criteria is lowered, a greater percentage of the diseased will have a positive test, but so will some individuals without disease. When the cutoff criteria is very low, almost all of the diseased will have a positive test, but so will many of the nondiseased. The area under the ROC curve reflects the extent to which the test separates out the diseased from the nondiseased.
By plotting the TP percentage (sensitivity) against the FP percentage (1 – specificity) for three different cutoff criteria, Figure 4 illustrates the construction of an ROC curve.
When the cutoff criteria is at point A of the test result curve (Figure 4, graph on left), approximately 50% of the diseased will have a positive test (sensitivity) and none of the nondiseased will have a positive test (zero FP). Therefore, point A on the ROC curve (Figure 4, graph on right) will be halfway up the Y-axis, which represents the percentage of TP.
When the cutoff criteria is at point B of the test result curve (Figure 4, graph on left), approximately 70% of the diseased will have a positive test (sensitivity), but so do approximately 10% of the nondiseased. Therefore, point B on the ROC (Figure 4, graph on right) curve will be at 70% up the Y-axis (TP) and 10% on the X-axis (FP).
Finally, when the cutoff criteria is at point C on the test result curve (Figure 4, graph on left), about 90% of the diseased will have a positive test (sensitivity) and so will about 30% of the nondiseased. Therefore, point C on the ROC curve (Figure 4, graph on right) will be at 90% on the Y-axis (TP) and 30% on the X-axis (FP).
A perfect test would identify all of the diseased and reach 100% on the Y-axis (TP axis) before any FPs occurred. In this case, the ROC curve would proceed straight up the Y-axis (TP axis) and to the right, forming a right angle. The area under this curve would be 1.00.
If the diseased population and the nondiseased populations were exactly the same, the ROC curve would proceed in a straight line at a 45-degree angle starting at the origin. At every cutoff point, the same percentage of diseased (TP) and nondiseased (FP) would be identified. The area under such a curve would be 0.5. Such a test would be no better than a coin flip. The 45-degree line is sometimes referred to as the “coin-flip” ROC curve.
Therefore, the greater the area under the ROC curve, the better the test is at discriminating between the diseased and the nondiseased. This area is also called the C (concordance) statistic.
If one were at point B on an ROC curve and the cutoff criteria were then made more sensitive, would the next likely point on the ROC curve be point A or C? To respond to this question, it is important to realize that if the cutoff criteria were made more sensitive, a greater proportion of the diseased would have a positive test. Therefore, the TP value would be higher. Point C has a higher TP value, which makes it the correct answer.
LIKELIHOOD RATIO AND APPLICATION USING STORY-LIKE FORMAT
The likelihood ratio (LR) offers a convenient way to make processes we do every day in medicine (eg, history taking, conducting a physical examination, laboratory testing) more mathematically precise. LR can be positive or negative. A positive LR is the ratio of the probability of having a positive test in the individual who has the disease in question divided by the probability of having a positive test in the individual who does not have the disease in question. The probability of having a positive test if disease is present is simply the sensitivity of the test. The probability of having a positive test if the disease is not present is 1 – specificity of the test (the FP). On the contrary, a negative LR is the ratio of the probability of having a negative test in the individual who has the disease in question divided by the probability of having a negative test in the individual who does not have the disease in question. The probability of having a negative test if disease is present is 1-sensitivity, and the probability of having a negative test if the disease is absent is the specificity.
For example, suppose two people come to the emergency department complaining of chest pain. One person is in their mid-60s with hypertension, a lifelong smoker who does not exercise, and has pronounced visceral adiposity. The other is a healthy 30-year-old never smoker, without family history of premature coronary heart disease, and who exercises regularly. Let us further suppose that each performed and had a positive treadmill stress test. What is the likelihood that either (or both) of them has significant coronary heart disease?
The positive likelihood ratio for the treadmill stress test will give us extremely helpful information in this situation. When the likelihood ratio is multiplied by the “prior odds” of having disease, as determined before the test is done, that gives the “posterior odds” or the odds of having the disease given that the test is positive, represented by the formula: Prior Odds x Likelihood Ratio = Posterior Odds
Let us apply this approach to our two patients with chest pain. First, we must estimate the prior odds of coronary disease for each patient. For the individual in their mid-60s, we may reasonably estimate that the probability of chest pain due to coronary disease may be approximately 75%, or a prior odds of 3:1. For the younger individual, we may estimate that the prior probability of coronary disease is approximately 0.1% (1 in a 1000), or a prior odds of 1:999, since otherwise healthy young individuals rarely have symptomatic coronary artery disease.5
Next, what is the positive likelihood ratio of a treadmill stress test? Suppose that both the sensitivity and specificity of this test – for both patients – is 75%. Based on the test characteristics, the positive likelihood ratio would be sensitivity/(1 – specificity) or 0.75/(1 – 0.75), which is 0.75/0.25, or 3.
For the older individual, prior odds multiplied by LR equals 9:1 (3:1 x 3:1 = 9:1). The posterior odds are 9:1. Odds of 9:1 represent a probability of 9/(9 + 1) = 9/10, or 90%. Therefore, the positive stress test increased our estimate of the probability of the older individual having coronary disease from 75% (pretest) to 90% (posttest). The pretest probability of 75% may make you wonder why the patient went for a stress test instead of a coronary angiogram, considered a definitive test.
What about the young individual? The prior odds were 1:999. When multiplied by the likelihood ratio for a positive stress test (3:1), we arrive at a posterior odds of 3:999, or a posterior probability of 0.3%. Since the prior probability of coronary disease in the young individual was low, having a positive stress test does not add additional information, and it is highly likely to be a FP test.
This example is similar in many other diagnostic situations. For example, if you hear an isolated crackle in the lung of an otherwise healthy patient, it probably does not mean much. However, if you hear the same crackle in the lung of a cachectic patient with a temperature of 104 °F, a respiratory rate of 35 per minute, and a heart rate of 110 beats per minute, you should be thinking about pneumonia.6
The breast cancer question that Gigerenzer posed also can be solved using LRs. Since the prevalence of breast cancer was 0.8%, the prior odds of breast cancer were 8:992. Since the sensitivity of mammography was 90% and the FP rate 7%, the LR positive (or sensitivity divided by 1 – specificity) was 0.90/0.07, or 12.9. The posterior odds are prior odds multiplied by the LR = 8/992 x 12.9 = 7.2/69.4. The posterior probability is 7.2/(7.2 + 69.4) = 9.4%. Notice, the 9.4% is same as was calculated with the story-like approach, neglecting rounding errors.
How are LRs interpreted? As rules of thumb, assuming complete equipoise (a prior odds of 1:1, ie, 50% probability) a positive LR of 2 increases the probability of the disease in question by about 15%, an LR of 5 by about 30%, and an LR of 10 by about 40%. An LR >10 is considered strong evidence for a disease. Similarly, a negative LR of 0.5 reduces the probability of disease by about 15%, an LR of 0.2 by about 30%, and an LR of 0.1 by about 40%. An LR of <0.1 is considered strong evidence against a disease.
In summary, the LR (positive or negative) helps us refine our estimate of some disease. It is algebraically identical to the story-like format for Bayes’ rule discussed above. It is simply another way to apply Bayes’ rule, and it is used when thinking about how much information a positive or negative test would add to our estimate of disease.
LIKELIHOOD RATIOS AND ILLNESS SCRIPT ENRICHMENT
Understanding script theory is a key component of diagnostic reasoning. An illness script is an individual’s organized mental model of a disease state. The information is organized in domains: epidemiology, pathophysiology, signs and symptoms, diagnostics, therapeutics, and prognosis. Novice learners begin building their script with biomedical knowledge, often gleaned from textbooks. By seeing more patients with varied presentations of diseases and deliberately practicing medicine, more experienced learners mature their illness scripts and build tolerance for ambiguity.
Over time, learners accumulate clinical experience that contributes to knowledge of diseases, and their corresponding illness scripts will be refined. In the case of physical examination findings or diagnostic testing for a disease, understanding their operating characteristic (such as LR) proffers an opportunity to add precision to biomedical and clinical knowledge. For instance, a novice learner’s illness script for acute bacterial meningitis may include the commonly taught Kernig’s and Brudzinski’s signs, which were described over a century ago in patients with late-stage bacterial and tuberculous meningitis.7 A study evaluating the utility of these signs in acute bacterial meningitis found they lacked diagnostic value: both signs were found to have a sensitivity of 5% and a positive LR of 0.97, akin to flipping a coin.8 Informed with new information, learners can refine their “signs and symptoms” domain of the acute bacterial meningitis illness script to include more precise (LR-based) estimates of diagnostic value for the Kernig and Brudzinski maneuvers.
In all cases, probabilistic thinking is needed to interpret diagnostic tests. For that reason, the next article in this series will discuss probability and its relationship to statistics.
SUMMARY
- The operating characteristics of a test reflect how well a test identifies those with a disease (sensitivity) and those without the disease (specificity).
- If the disease prevalence is known, Gigerenzer’s story-like format is a simple way to apply Bayes’ Rule to determine the probability that a person has a disease given a PPV.
- The ROC curve is a graphical means to demonstrate how well a test separates out the diseased from the nondiseased. The greater the area under the ROC curve, the better the test discriminates between the diseased and the nondiseased.
- If the prevalence of the disease is not known, as is common in clinical practice, the LR approach is mathematically identical to the story-like approach. In this case, the estimate of the prior odds serves as an estimate of the disease prevalence. As noted, some commonly accepted clinical tests have an LR of approximately 1, which is equivalent to a “coin flip.”
- As learners accrue knowledge, the LR for physical examination findings and diagnostic tests adds precision to their illness scripts.
- In all cases, probabilistic thinking is needed to interpret diagnostic tests. For that reason, the next article in this series will discuss probability and its relationship to statistics.
REFERENCES
- Stigler SM. The History of Statistics. Belknap Press; 1986:88,97-98.
- Gigerenzer G. Calculated Risks: How To Know When Numbers Deceive You. Simon and Shuster; 2002:40-49.
- Cohen JF, Bertille N, Cohen R. Rapid antigen detection test for group A streptococcus in children with pharyngitis. Cochrane Database of Systematic Reviews. 2016;7(7):CD010502. doi:10.1002/14651858.CD010502.pub2.
- Junge MRJ, Dettori JR. ROC solid: receiver operator characteristic (ROC) Curves as a foundation for better diagnostic tests. Global Spine J. 2018;8(4):424-429. doi:10.1177/2192568218778294
- Kahn SS, Coresh J, Pencina MJ, et al. Novel prediction equations for absolute risk assessment of total cardiovascular disease incorporating cardiovascular-kidney-metabolic health: a scientific statement from the American Heart Association. Circulation. 2023;148(24):1982-2004. doi:10.1161/CIR.0000000000001191
- McGee S. Evidence-Based Physical Diagnosis. 4th ed. Elsevier; 2017.
- Forgie SE. The history and current relevance of the eponymous signs of meningitis. Pediatr Infect Dis J. 2016;35(7):749-751. doi:10.1097/INF.0000000000001152
- Thomas KE, Hasbun R, Jekel J, Quagliarello VJ. The diagnostic accuracy of Kernig’s sign, Brudzinski’s sign, and nuchal rigidity in adults with suspected meningitis. Clin Infect Dis. 2002;35(1):46-52. doi:10.1086/340979